하노이의 탑 기본 개념
하노이의 탑은 작은 원반이 위에, 큰 원반이 아래에 위치하는 규칙을 지키면서 기둥 3개를 이용해서 원반을 옮기는 문제이다.
먼저 크기가 모두 다른 원반이 첫 번째 기둥에 쌓여 있는 상태로 시작한다(이때 작은 원반은 위에, 큰 원반은 아래에 있다.)
이 상태에서 모든 원반을 세 번째 기둥에 최소 횟수로 옮기면 된다.
원반은 1개씩 옮길 수 있으며 큰 원반은 작은 원반 위에 쌓을 수 없다.

원반이 3개일 때
원반을 그룹으로 묶어서 옮기는 과정을 살펴보자(그룹으로 묶는 이유는 위에서 살펴봤듯이 어차피 가장 하단에 있는 원반을 제외한 나머지 원반들이 옮겨지는 과정은 동일하기 때문이다.)
원반 1과 원반 2를 그룹으로 묶으면 가장 먼저 이 그룹을 중간 기둥으로 옮긴 후에 가장 큰 원반 3을 목표 기둥으로 옮기면 된다. 그러면 총 3단계로 이동할 수 있다.

원반이 2개일 때
원반 1과 원반 2를 묶은 그룹을 풀어서 옮기는 단계를 어떻게 구현할지 생각해야 한다.
아래 그림은 원반 1과 원반 2의 이동 과정을 보여준다.
원반 1을 그룹으로 본다면 원반이 3개일 때와 똑같이 3단계로 이동할 수 있다.

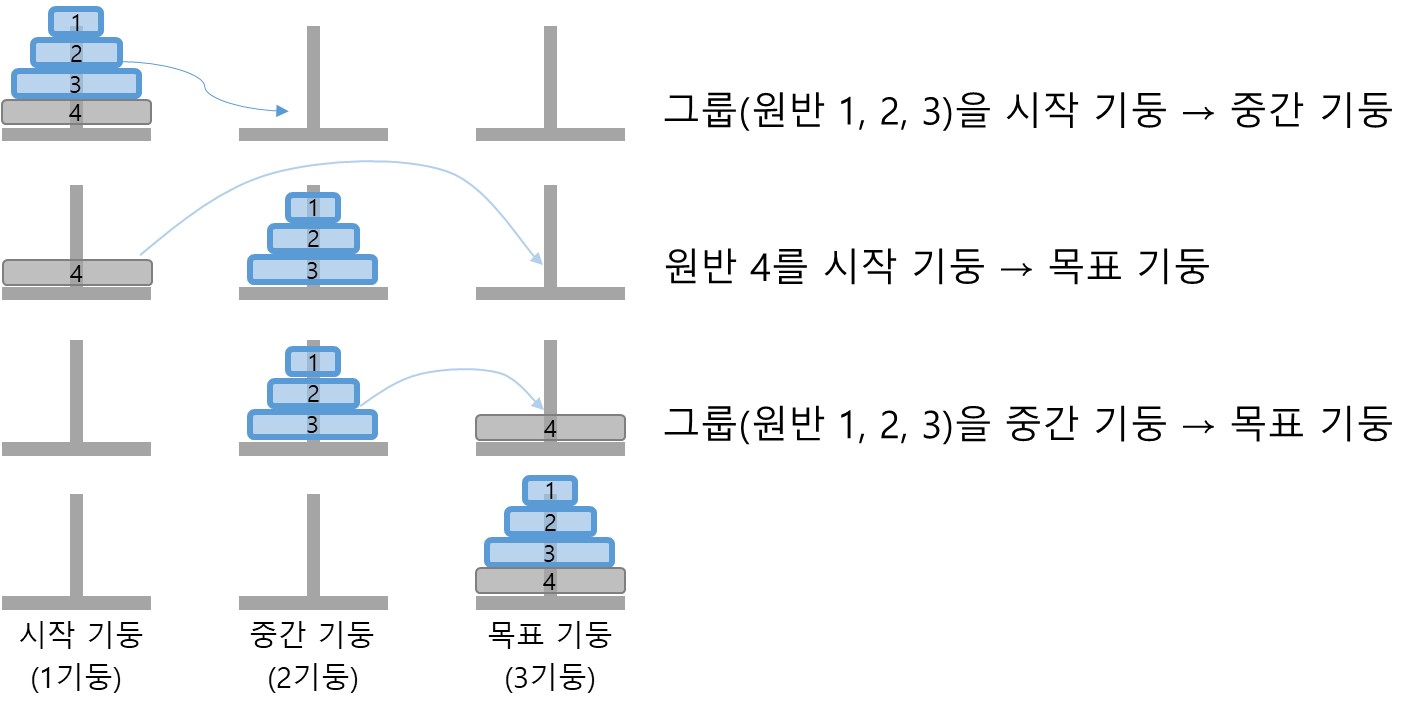
원반이 4개일 때
원반이 4개일 때도 방법은 똑같다.
2개, 3개일 때와 같이 원반 1, 원반 2, 원반 3을 그룹으로 묶으면 3단계로 이동할 수 있다. 그리고 다시 원반 3개를 묶었던 그룹을 풀어서 옮기면 된다.
이 과정을 통하여 원반이 n개인 하노이의 탑 문제를 해결할 수 있다.
하노이의 탑을 구현하는 프로그램
move( ) 함수의 매개변수 no는 옮겨야 할 원반의 개수, x는 시작 기둥의 번호, y는 목표 기둥의 번호이다.
# 하노이의 탑 구현하기
def move(no: int, x: int, y: int) -> None:
"""원반 no개를 x기둥에서 y기둥으로 옮김"""
if no > 1:
move(no - 1, x, 6 - x - y)
print(f'원반 [{no}]을(를) {x}기둥에서 {y}기둥으로 옮깁니다.')
if no > 1:
move(no - 1, 6 - x - y, y)
print('하노이의 탑을 구현합니다.')
n = int(input('원반의 개수를 입력하세요.: '))
move(n, 1, 3) # 1기둥에 쌓인 원반 n개를 3기둥으로 옮김
실행 결과
하노이의 탑을 구현합니다.
원반의 개수를 입력하세요.: 3
원반 [1]을(를) 1기둥에서 3기둥으로 옮깁니다.
원반 [2]을(를) 1기둥에서 2기둥으로 옮깁니다.
원반 [1]을(를) 3기둥에서 2기둥으로 옮깁니다.
원반 [3]을(를) 1기둥에서 3기둥으로 옮깁니다.
원반 [1]을(를) 2기둥에서 1기둥으로 옮깁니다.
원반 [2]을(를) 2기둥에서 3기둥으로 옮깁니다.
원반 [1]을(를) 1기둥에서 3기둥으로 옮깁니다.
Process finished with exit code 0
이 프로그램에서는 기둥 번호를 정숫값 1, 2, 3으로 나타낸다. 기둥 번호의 합이 6이므로 시작 기둥, 목표 기둥이 어느 위치에 있든 중간 기둥은 (6 - x - y)로 구할 수 있다.
move( ) 함수는 no개의 원반을 다음과 같은 과정으로 이동한다.
- 바닥에 있는 원반을 제외한 그룹(원반[1]~원반[no - 1])을 1기둥에서 2기둥으로 옮긴다.
- 바닥에 있는 원반 [no]를 1기둥에서 3기둥으로 옮겼다는 것을 출력한다.
- 바닥에 있는 원반을 제외한 그룹(원반[1]~원반[no - 1])을 2기둥에서 3기둥으로 옮긴다.
위 1, 3 과정은 재귀 호출로 구현한다. no가 3일 때 move( ) 함수의 동작을 아래 그림과 같이 나타낼 수 있다.
