지난 글에서 퀵 정렬에 대해 살펴보았다.
[정렬 알고리즘] 퀵 정렬
퀵 정렬이란? - 일반적으로 사용되는 아주 빠른(quick) 정렬 알고리즘 - Charles A. R Hoare에 의해 고안됨 - 중심 축이 되는 값(피벗)을 선택하여 그룹을 나누어가는 방법 - 재귀적으로 호출하여 진행하
vibeee.tistory.com
퀵 정렬에서의 피벗
퀵 정렬의 경우 피벗을 선택하는 방법에 따라 성능이 달라지기 때문에 결국 피벗을 선택하는 방법이 성능을 좌우한다고 볼 수 있다.
아래 예시를 통해 피벗을 선택하는 예시를 살펴보자.

먼저 위와 같은 배열이 있을 때, 맨 앞 원소(8)를 선택한다고 해보자.
만약 8이 피벗으로 선택된다면, 0~7과 8이 있는 두 가지 그룹으로 나눌 수 있다.
이렇게 나누어지게 된다면 한쪽으로 완전히 치우쳐진 분할을 반복하기 때문에 빠른 정렬 속도를 기대할 수 없다.
또 하나 예를 들어보면 배열을 정렬한 뒤 가운데에 위치하는 값, 즉 전체에서 중앙값을 피벗으로 선택하게 된다면 어떨까?
배열이 한쪽으로 치우치지 않고 절반 크기로 나누어져 이상적인 정렬의 효과를 기대할 수 있다.
하지만 정렬된 배열에서 중앙값을 구하려면 그에 대한 처리가 필요하고, 많은 계산 시간을 소모하기 때문에 결국 피벗을 선택하는 의미가 없어진다.
피벗을 선택하는 방법 2가지
방법 1) 나누어야 할 배열의 원소 수가 3 이상이면, 배열에서 임의의 원소 3개를 꺼내 중앙값인 원소를 피벗으로 선택한다.
-> 맨 앞 원소(8), 가운데 원소(4), 맨 끝 원소(0) 중에서 중앙값인 4를 피벗으로 선택하면 치우치지 않고 나눌 수 있다.

방법 2-1) 나누어야 할 배열의 맨 앞 원소, 가운데 원소, 맨 끝 원소를 정렬한다.
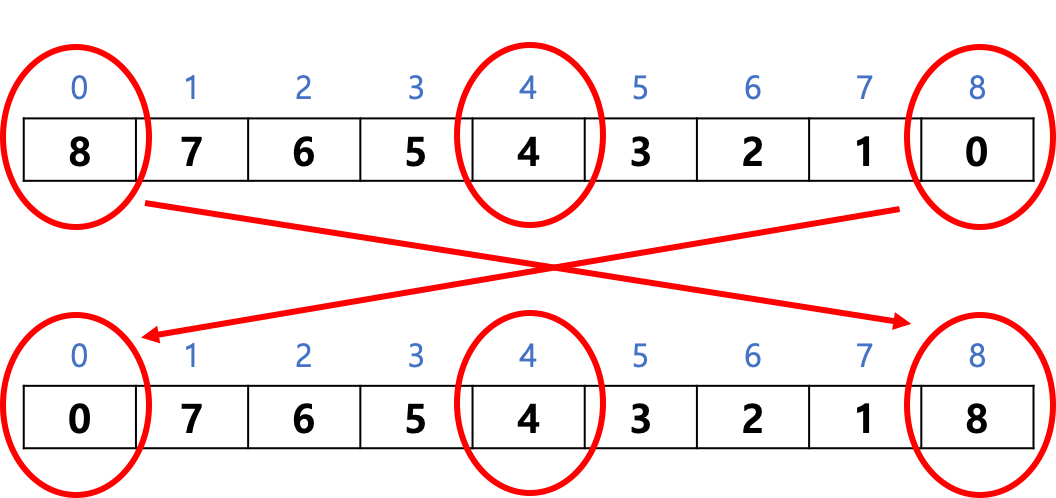
방법 2-2) 가운데 원소와 맨 끝에서 두 번째 원소를 교환한 후 맨 끝에서 두 번째 원솟값 a[right - 1]이 피벗으로 선택한다.

방법 2-3) 그룹으로 나눌 대상을 a[left + 1] ~ a[right - 2]로 좁힌다.

이 과정을 거치고 나면 스캔할 커서의 시작 위치(pl, pr)를 다음과 같이 변경하여 나눌 대상 범위를 좁힐 수 있다.
- 왼쪽 커서 pl의 시작 위치: left → left + 1
- 오른쪽 커서 pr의 시작 위치: right → right - 2
방법 2를 적용하여 구현한 코드
def select_value(arr, idx1, idx2, idx3):
if arr[idx2] < arr[idx1]: arr[idx2], arr[idx1] = arr[idx1], arr[idx2]
if arr[idx3] < arr[idx2]: arr[idx3], arr[idx2] = arr[idx2], arr[idx3]
if arr[idx2] < arr[idx1]: arr[idx2], arr[idx1] = arr[idx1], arr[idx2]
return idx2
def qsort(arr, left, right):
pl = left # 왼쪽 포인터 pl
pr = right # 오른쪽 포인터 pr
middle = select_value(arr, pl, (pl + pr) // 2, pr) # 중앙값 인덱스 반환
pivot = arr[middle] # 피벗 pivot
arr[middle], arr[pr - 1] = arr[pr - 1], arr[middle] # 중앙값과 pr - 1 값 교환
pl += 1 # pl의 시작 위치 변경
pr -= 2 # pr의 시작 위치 변경
while pl <= pr:
while arr[pl] < pivot: pl += 1
while arr[pr] > pivot: pr -= 1
if pl <= pr:
arr[pl], arr[pr] = arr[pr], arr[pl]
pl += 1
pr -= 1
if left < pr: qsort(arr, left, pr) # pr이 a[0]보다 오른쪽에 위치하면 왼쪽 그룹 나누기
if pl < right: qsort(arr, pl, right) # pl이 a[8]보다 왼쪽에 위치하면 오른쪽 그룹 나누기
def quick_sort(arr):
qsort(arr, 0, len(arr) - 1)
print("퀵 정렬을 수행합니다.")
num = int(input("원소 수를 입력하세요.: "))
array = [None] * num
for i in range(num):
array[i] = int(input(f"array[{i}]: "))
quick_sort(array)
print("오름차순으로 정렬했습니다.")
for i in range(num):
print(f"array[{i}] = {array[i]}")⭐️ 위 방법을 사용하면 나누는 그룹이 한쪽으로 치우치는 것을 방지할 수 있고, 스캔할 원소를 3개 줄일 수 있으므로, 이 방법을 사용하지 않을 때보다 조금 더 빠른 속도로 정렬할 수 있다.
퀵 정렬의 시간 복잡도와 삽입 정렬로 전환하기
퀵 정렬의 일반적으로 알려져있는 시간 복잡도는 O(n log n)이다. 하지만 위와 같이 정렬하는 배열의 초깃값이나 피벗을 선택하는 방법에 따라서 실행시간 복잡도가 증가하는 경우도 있다. 예를 들어 매번 1개의 원소와 나머지 원소로 나누어진다면 n번의 분할이 필요해지기 때문에 최악의 시간복잡도인 O(n^2)이 된다.
따라서 원소 수가 적을때는 아래 코드와 같이 퀵 정렬이 아닌 삽입 정렬로 전환하여 실행하면 효율적으로 정렬을 수행할 수가 있다.
def select_value(arr, idx1, idx2, idx3):
if arr[idx2] < arr[idx1]: arr[idx2], arr[idx1] = arr[idx1], arr[idx2]
if arr[idx3] < arr[idx2]: arr[idx3], arr[idx2] = arr[idx2], arr[idx3]
if arr[idx2] < arr[idx1]: arr[idx2], arr[idx1] = arr[idx1], arr[idx2]
return idx2
def insertion_sort(arr, left, right):
for i in range(left + 1, right + 1):
j = i
tmp = arr[i]
while j > 0 and arr[j - 1] > tmp:
arr[j] = arr[j - 1]
j -= 1
arr[j] = tmp
def qsort(arr, left, right):
if right - left < 9: # 원소 수가 9 미만이면 단순 삽입 정렬로 전환
insertion_sort(arr, left, right)
else:
pl = left # 왼쪽 포인터 pl
pr = right # 오른쪽 포인터 pr
middle = select_value(arr, pl, (pl + pr) // 2, pr) # 중앙값 인덱스 반환
pivot = arr[middle] # 피벗 pivot
arr[middle], arr[pr - 1] = arr[pr - 1], arr[middle] # 중앙값과 pr - 1 값 교환
pl += 1 # pl의 시작 위치 변경
pr -= 2 # pr의 시작 위치 변경
while pl <= pr:
while arr[pl] < pivot: pl += 1
while arr[pr] > pivot: pr -= 1
if pl <= pr:
arr[pl], arr[pr] = arr[pr], arr[pl]
pl += 1
pr -= 1
if left < pr: qsort(arr, left, pr) # pr이 a[0]보다 오른쪽에 위치하면 왼쪽 그룹 나누기
if pl < right: qsort(arr, pl, right) # pl이 a[8]보다 왼쪽에 위치하면 오른쪽 그룹 나누기
def quick_sort(arr):
qsort(arr, 0, len(arr) - 1)
print("퀵 정렬을 수행합니다.(원소 수가 9 미만이면 단순 삽입 정렬을 합니다)")
num = int(input("원소 수를 입력하세요.: "))
array = [None] * num
for i in range(num):
array[i] = int(input(f"array[{i}]: "))
quick_sort(array)
print("오름차순으로 정렬했습니다.")
for i in range(num):
print(f"array[{i}] = {array[i]}")
sorted( ) 함수의 사용
a, b = sorted([a, b]) # a, b를 오름차순으로 정렬
a, b, c = sorted([a, b, c]) # a, b, c를 오름차순으로 정렬
a, b, c, d = sorted([a, b, c, d]) # a, b, c, d를 오름차순으로 정렬
a, b = sorted([a, b], reverse = True) # a, b를 오름차순으로 정렬
a, b, c = sorted([a, b, c], reverse = True) # a, b, c를 오름차순으로 정렬
a, b, c, d = sorted([a, b, c, d], reverse = True) # a, b, c, d를 오름차순으로 정렬위 예시에서는 변수를 나열한 리스트를 sorted( ) 함수에 전달하고, 반환된 리스트를 풀어서 변수에 대입한다.
sorted( ) 함수는 오름차순을 기본으로 하지만, reverse에 True 값을 넘겨주면 내림차순 정렬을 수행한다.
하지만 튜플은 이뮤터블의 속성(값이 변하지 않음)을 가지므로 튜플 자체를 정렬할 때는 다음과 같은 방법을 사용해야 한다.
- 1단계: sorted( ) 함수로 정렬한 원소의 나열에서 새로운 리스트를 생성한다.
- 2단계: 생성한 리스트를 튜플로 반환한다.
>>> x = (1, 3, 2)
>>> x = tuple(sorted(x))
>>> x
(1, 2, 3)
'자료구조, 알고리즘 입문 > 정렬 알고리즘' 카테고리의 다른 글
| [정렬 알고리즘] 병합 정렬(합병 정렬, 머지 소트, 머지 정렬) (1) | 2024.09.24 |
|---|---|
| [정렬 알고리즘] 퀵 정렬 (3) | 2024.09.22 |
| [정렬 알고리즘] 단순 삽입 정렬(셔틀 정렬), 이진 삽입 정렬 (0) | 2022.05.26 |
| [알고리즘] 단순 선택 정렬 (0) | 2022.05.23 |
| [알고리즘] 셰이커 정렬, 파이썬 내장 함수 (0) | 2022.05.19 |