병합 정렬이란?
- 배열을 앞부분과 뒷부분의 두 그룹으로 나누어 각각 정렬한 후 병합하는 작업을 반복(재귀)
- 퀵 정렬과 다르게 피벗값이 존재하지 않음(배열 항상 반으로 쪼개기 때문)
- 병합할 때 2의 배수만큼 병합함
- 시간 복잡도는 O(n log n) 을 보장
- 작업용 배열을 생성할 때 추가적인 데이터 공간이 필요하므로 메모리 활용면에서는 비효율적이라는 문제가 있음
정렬을 마친 두 배열의 병합 과정
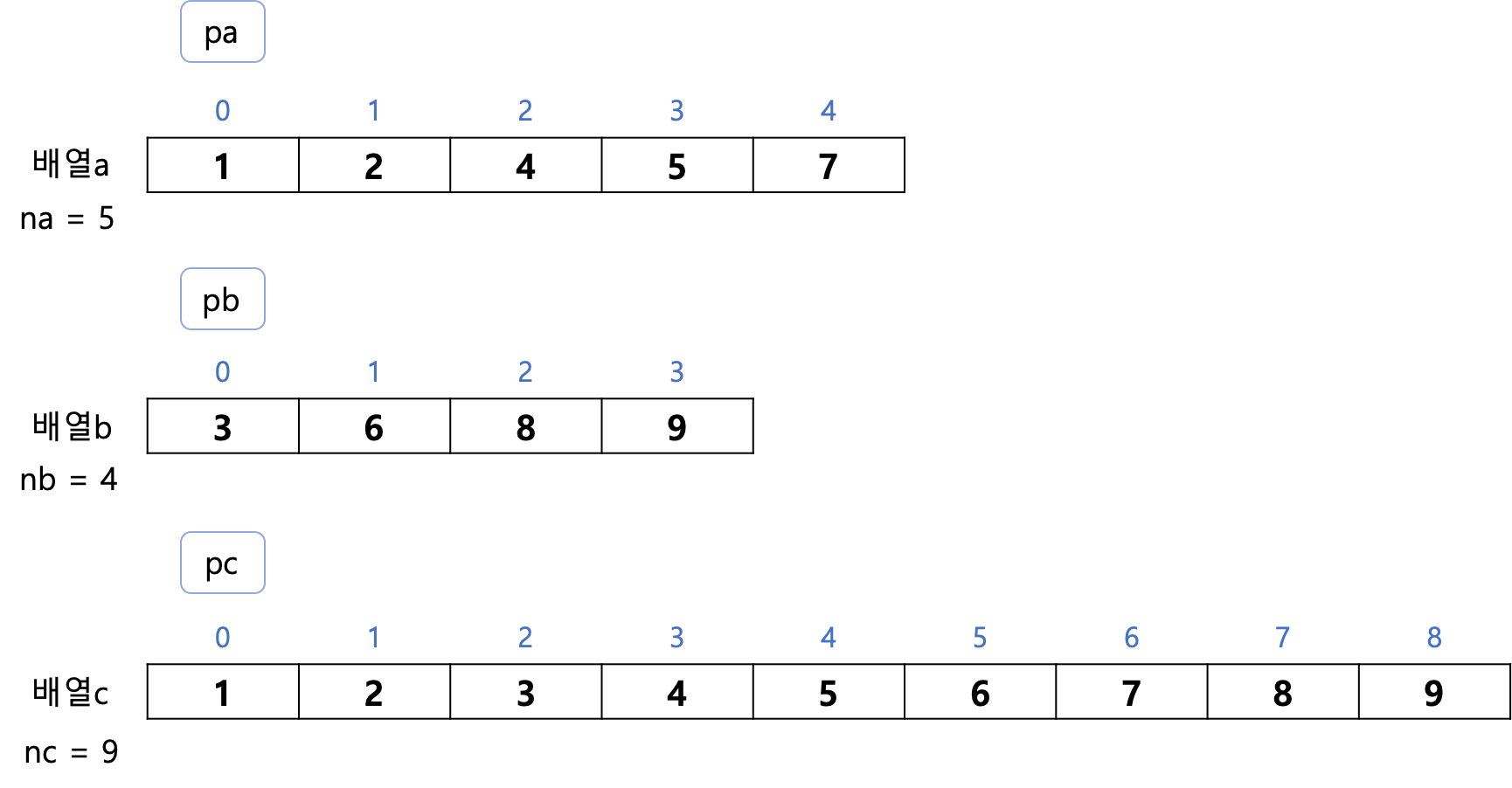
병합을 마치면 위와 같이 정렬이 완료되는데 그 과정을 자세히 들여다 보면 세 가지 과정으로 수행된다.
1) 각 배열의 커서인 pa, pb, pc를 만들고 각각 0을 저장, 각 배열의 원소 수를 담는 na, nb, nc를 만들고 원소의 길이를 저장.
2) pa와 pb를 비교하여 작은 값을 pc에 저장. pa가 작다면 pc에 pa를 담아주고 pa와 pc를 한 칸씩 이동, pb가 작다면 pc에 pb를 담아주고 pb와 pc를 한 칸 이동.
3) 배열 a 또는 배열 b에 남은 원소를 배열 c에 복사. 위 예시에서는 배열 a의 길이가 1만큼 더 길기때문에 복사 후 pa와 pc를 한 칸 이동.
정렬을 마친 두 배열을 병합하는 코드
위 과정을 코드로 옮기면 다음과 같이 나타낼 수 있다.
# 정렬을 마친 두 배열을 병합하기
from typing import Sequence, MutableSequence
def merge_sorted_list(a: Sequence, b: Sequence, c: MutableSequence) -> None:
"""정렬을 마친 배열 a와 b를 병합하여 c에 저장"""
pa, pb, pc = 0, 0, 0 # 각 배열의 커서
na, nb, nc = len(a), len(b), len(c) # 각 배열의 원소 수
while pa < na and pb < nb: # pa와 pb를 비교하여 작은 값을 pc에 저장
if a[pa] <= b[pb]:
c[pc] = a[pa]
pa += 1
else:
c[pc] = b[pb]
pb += 1
pc += 1
while pa < na: # a에 남은 원소를 c에 복사
c[pc] = a[pa]
pa += 1
pc += 1
while pb < nb: # b에 남은 원소를 c에 복사
c[pc] = b[pb]
pb += 1
pc += 1
if __name__ == "__main__":
a = [2, 4, 6, 8, 11, 13]
b = [1, 2, 3, 4, 9, 16, 21]
c = [None] * (len(a) + len(b))
print("정렬을 마친 두 배열의 병합을 수행합니다.")
merge_sorted_list(a, b, c) # 배열 a와 b를 병합하여 c에 저장
print('배열 a와 b를 병합하여 배열 c에 저장했습니다.')
print(f'배열 a: {a}')
print(f'배열 b: {b}')
print(f'배열 c: {c}')
10~17행: 첫 번째 while문 - 배열 a의 a[pa]와 배열 b의 b[pb]를 주목하여 이 가운데 작은 값을 c[pc]에 저장한다. 이어서 a, b, c 배열의 커서를 1씩 증가시킨다.
위 그림에서는 a[0]과 b[0]을 비교하여 작은 값 1을 c[0]에 대입한다. 이후 b와 c 배열의 커서 pb와 pc만 1칸씩 오른쪽으로 이동한다. 이때 값을 꺼내지 않은 배열 a의 커서 pa는 이동하지 않는다. 이처럼 a[pa]와 b[pb]를 비교하여 작은 값을 c[pc]에 대입하고, 꺼낸 쪽 배열의 커서와 배열 c의 커서를 이동하는 작업을 반복한다. 커서 pa와 pb가 각각 배열의 맨 끝에 도달하면 while 문이 종료된다.
19~22행: 두 번째 while문 - 이 while문은 앞에서 배열 b의 모든 원소를 배열 c로 복사했지만, 배열 a에 아직 복사하지 않은 원소가 있으면 실행된다. 즉, 커서 pa가 배열 a의 맨 끝에 도달하지 않은 경우이다. 커서를 이동시키면서 배열 a에 남은 원소를 배열 c에 복사한다.
24~27행: 세 번째 while문 - 이 while문은 앞에서 배열 a의 모든 원소를 배열 c로 복사했지만, 배열 b에 아직 복사하지 않은 원소가 있으면 실행된다. 즉, 커서 pb가 배열 b의 맨 끝에 도달하지 않은 경우이다. 커서를 이동시키면서 배열 b에 남은 모든 원소를 배열 c에 복사한다.
⭐️ 파이썬에서 제공하는 sorted( ) 함수를 사용하여 다음과 같이 병합할 수도 있다.
c = list(sorted(a + b))
하지만 위 방법은 속도가 느리다는 단점이 있으므로, 아래와 같이 heapq 모듈의 merge( ) 함수를 사용하면 빠르게 병합할 수 있다.
# 정렬을 마친 두 배열의 병합(heapq.merge 사용)
import heapq
a = [1, 2, 4, 5, 7]
b = [3, 6, 8, 9]
c = list(heapq.merge(a, b)) # 배열 a와 b를 병합하여 배열c에 저장
(... 생략 ...)
병합 정렬의 진행 과정
병합 정렬은 분할 정복법에 따라 배열을 앞부분과 뒷부분으로 나누어 정렬하는 것이 기본이다.
1) 우선 배열을 아래와 같이 나눈다.
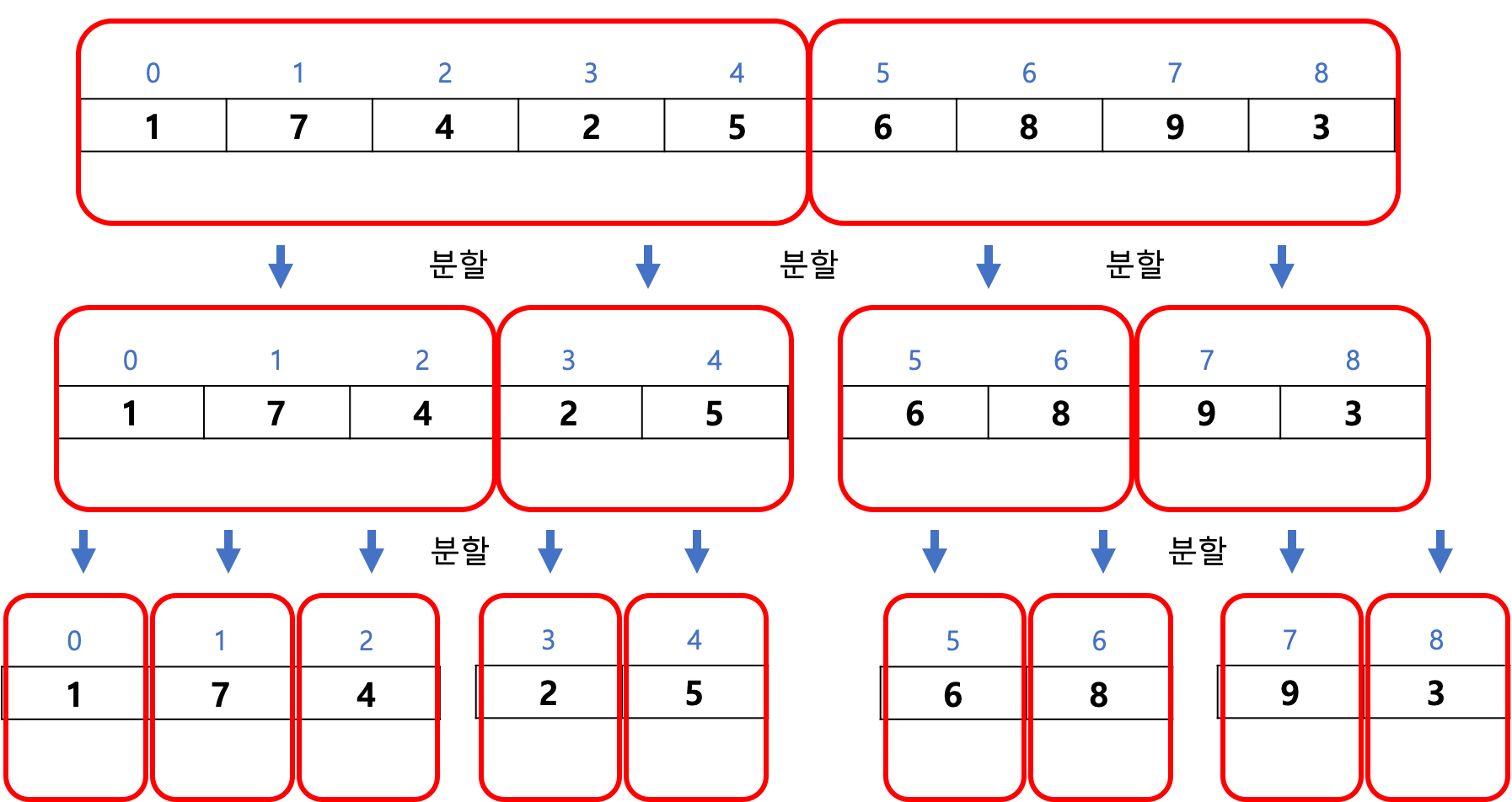
그럼 결국 1개의 배열 방에 1개의 원소만이 남게되고, 이 원소들을 다시 정렬하여 배열로 만들어주면 위의 그림과 같아진다.
이 배열들을 전부 정렬하고 병합하여 다시 원래의 배열에 옮겨 담아주는 순서가 아래 그림이다.
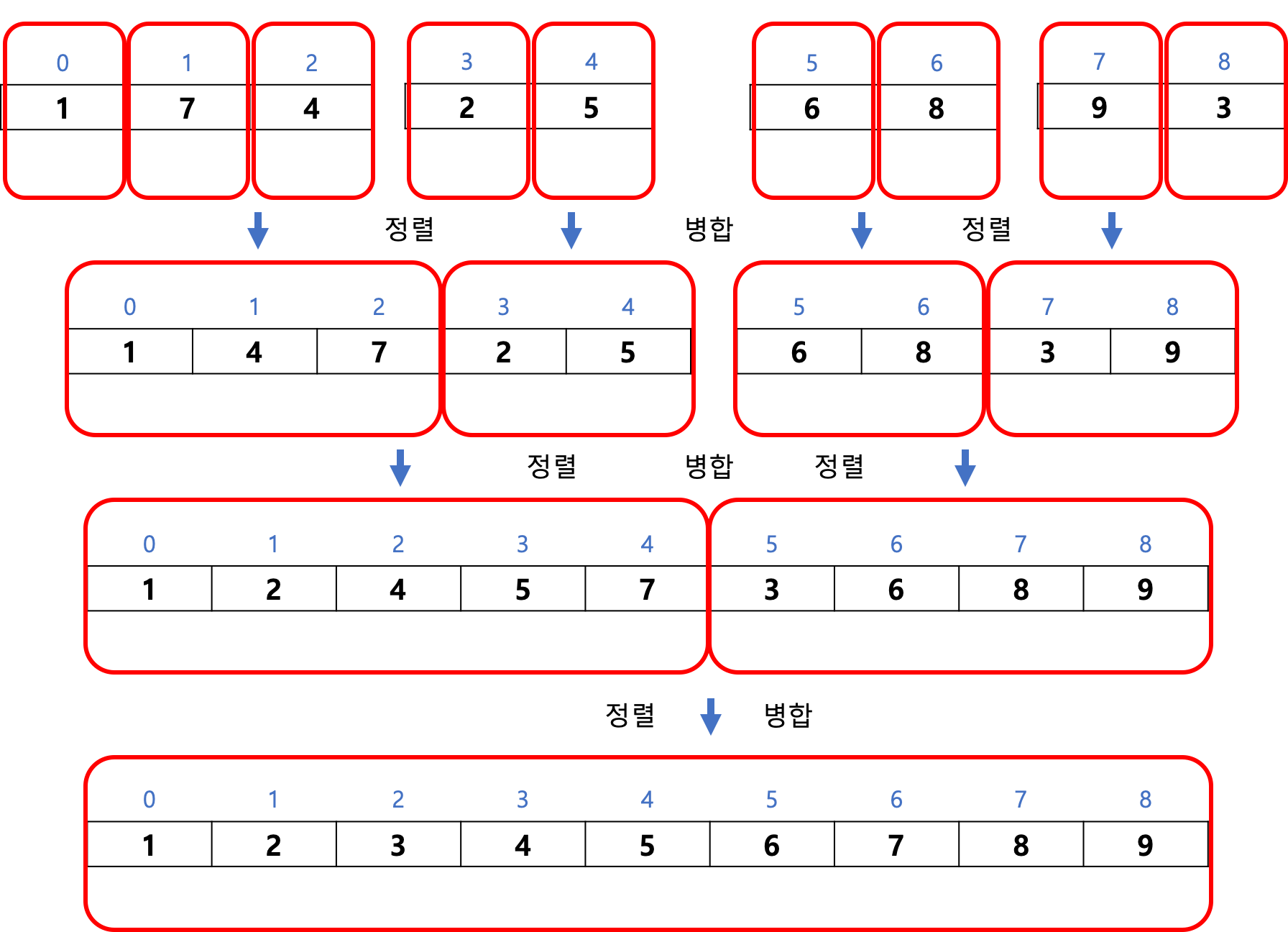
정렬하고 병합하는 과정을 마치게 되면 오름차순으로 병합정렬이 완료되는 것을 확인할 수 있다.
위 과정을 코드로 나타내면 다음과 같다.
병합 정렬 과정을 표현한 코드
# 병합 정렬 알고리즘 구현하기
from typing import MutableSequence
def merge_sort(a: MutableSequence) -> None:
"""병합 정렬"""
def _merge_sort(a: MutableSequence, left: int, right: int) -> None:
"""a[left] ~ a[right]를 재귀적으로 병합 정렬"""
if left < right:
center = (left + right) // 2
_merge_sort(a, left, center) # 배열 앞부분을 병합 정렬
_merge_sort(a, center + 1, right) # 배열 뒷부분을 병합 정렬
p = j = 0
i = k = left
while i <= center: # 배열 앞부분 복사
buff[p] = a[i]
p += 1
i += 1
while i <= right and j < p:
if buff[j] <= a[i]:
a[k] = buff[j]
j += 1
else:
a[k] = a[i]
i += 1
k += 1
while j < p:
a[k] = buff[j]
k += 1
j += 1
n = len(a)
buff = [None] * n # 작업용 배열을 생성
_merge_sort(a, 0, n - 1) # 배열 전체를 병합 정렬
del buff # 작업용 배열을 소멸
if __name__ == '__main__':
print('병합 정렬을 수행합니다.')
num = int(input('원소 수를 입력하세요.: '))
x = [None] * num # 원소 수가 num인 배열을 생성
for i in range(num):
x[i] = int(input(f'x[{i}]: '))
merge_sort(x) # 배열 x를 병합 정렬
print('오름차순으로 정렬했습니다.')
for i in range(num):
print(f'x[{i}] = {x[i]}')
실행 결과
병합 정렬을 수행합니다.
원소 수를 입력하세요.: 9
x[0]: 5
x[1]: 8
x[2]: 4
x[3]: 2
x[4]: 6
x[5]: 1
x[6]: 3
x[7]: 9
x[8]: 7
오름차순으로 정렬했습니다.
x[0] = 1
x[1] = 2
x[2] = 3
x[3] = 4
x[4] = 5
x[5] = 6
x[6] = 7
x[7] = 8
x[8] = 9
Process finished with exit code 0
위 코드를 통해 a[left] ~ a[right]를 재귀적으로 정렬하여 최종적으로 병합 정렬 된 배열을 출력한다.
⭐️ 배열 병합의 시간 복잡도는 O(n)이고, 데이터 원소 수가 n일 때 병합 정렬의 단계는 log n만큼 필요하므로 전체 시간 복잡도는 O(n log n)이다. 또한, 병합 정렬 알고리즘은 서로 떨어져 있는 원소를 교환하지 않으므로 안정적인 알고리즘이다.
'자료구조, 알고리즘 입문 > 정렬 알고리즘' 카테고리의 다른 글
| [정렬 알고리즘] 퀵 정렬 - 피벗을 선택하는 두 가지 방법 (0) | 2024.09.22 |
|---|---|
| [정렬 알고리즘] 퀵 정렬 (3) | 2024.09.22 |
| [정렬 알고리즘] 단순 삽입 정렬(셔틀 정렬), 이진 삽입 정렬 (0) | 2022.05.26 |
| [알고리즘] 단순 선택 정렬 (0) | 2022.05.23 |
| [알고리즘] 셰이커 정렬, 파이썬 내장 함수 (0) | 2022.05.19 |