[문자열 검색 알고리즘] 브루트 포스법

문자열 검색이란?

문자열 검색은 어떤 문자열 안에 다른 문자열이 포함되어 있는지 검사하고, 만약 포함되어 있다면 어디에 위치하는지 찾아내는 것

예를 들어 문자열 "STRING"에서 "IN"을 검색하면 성공하지만, 문자열 "QUEEN"에서 "IN"을 검색하면 실패함

문자열 검색에서 검색되는 쪽의 문자열을 텍스트(text), 찾아내는 문자열을 패턴(pattern)이라고 함

 

브루트 포스법이란?

문자열 검색 알고리즘 중 가장 기초적이고 단순한 알고리즘. 선형 검색을 단순하게 확장한 알고리즘이라서 단순법이라고 불린다.

텍스트 "ABABCDEFGHA"에서 패턴 "ABC"를 브루트 포스법으로 검색하는 순서는 다음과 같이 진행된다.

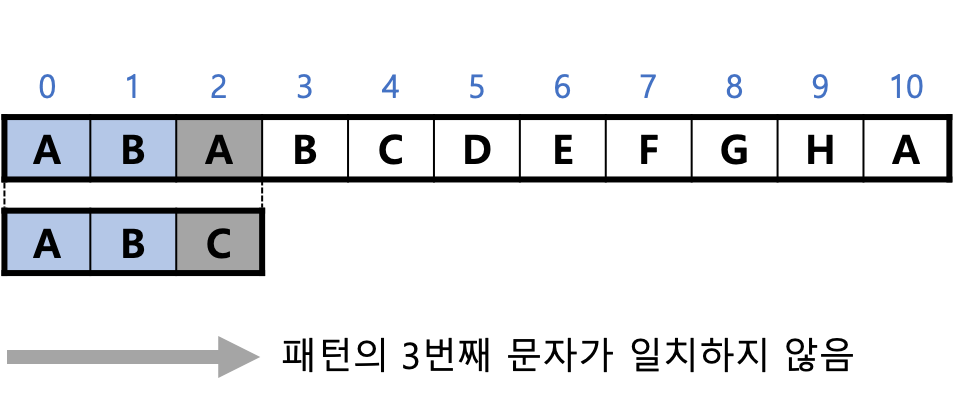
1. 텍스트의 첫 문자 "A"에서 시작하는 문자 3개가 패턴 "ABC"와 일치하는지 검사한다.

"A"와 "B"는 일치하지만 마지막 "C"가 일치하지 않으므로 패스한다.

 

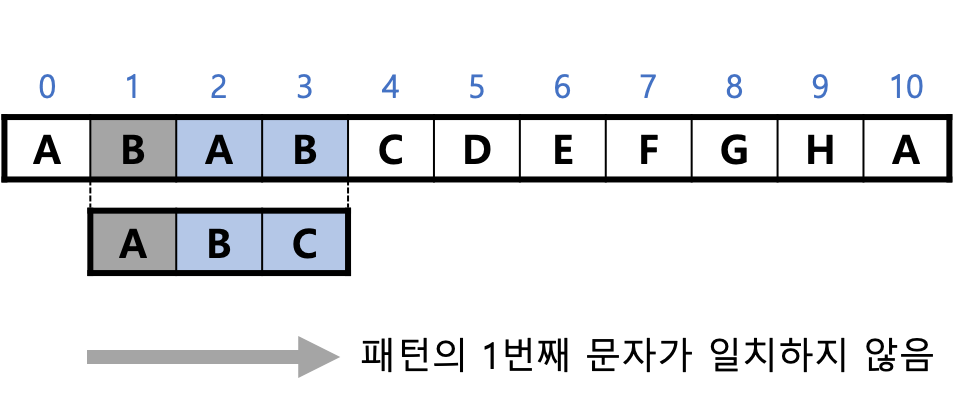
2. 패턴을 오른쪽으로 1칸 밀고, 텍스트의 2번째 문자와 그 이후 부분이 일치하는지 검사한다.

패턴의 첫 문자 "A"와 텍스트의 문자 "B"가 일치하지 않으므로 패스한다.

 

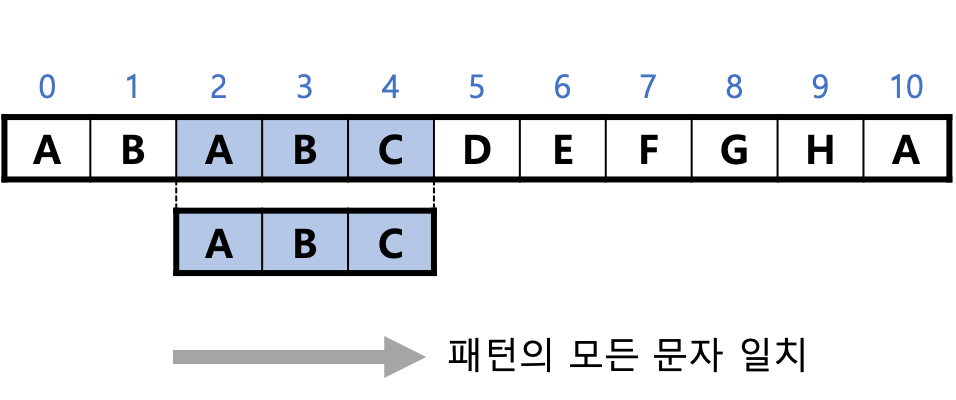
3. 패턴을 다시 오른쪽으로 1칸 밀고, 텍스트의 문자와 패턴의 문자가 일치하는지 검사한다.

패턴의 문자 "A", "B", "C"와 텍스트의 문자 "A", "B", "C"가 모두 일치하므로 검색에 성공한다.

 

이 알고리즘을 상세히 나타내면 다음과 같다.

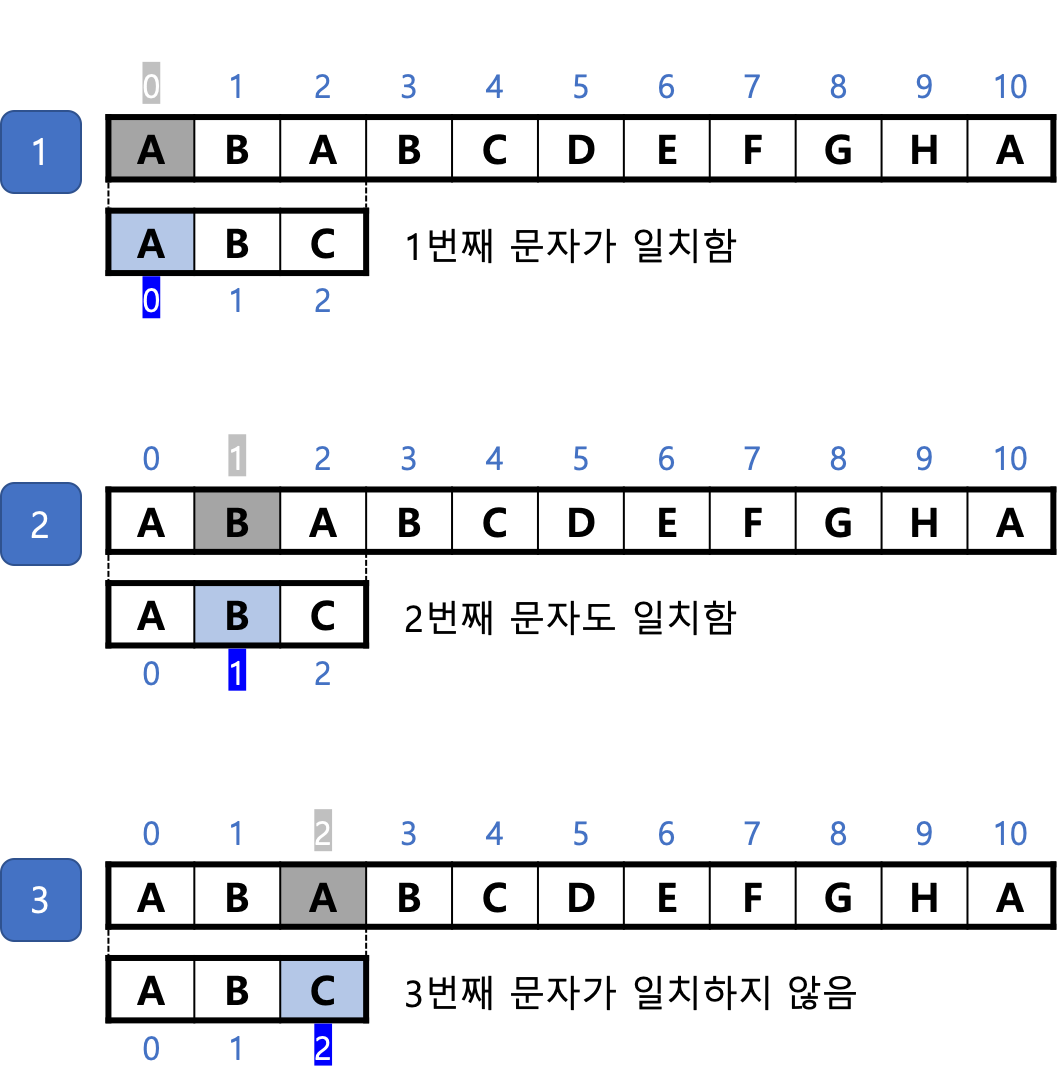
1. 텍스트와 패턴의 첫 문자를 위아래로 나란히 놓고 첫 문자부터 차례로 검사한다.

과정 1과 과정 2처럼 문자가 일치하는 동안은 계속 검사하다가 과정 3처럼 일치하지 않는 다른 문자를 만나면 더 이상 검사가 불필요하다고 판단하고 다음 단계로 넘어간다.

 

2. 과정 4의 패턴을 검사하는 시작 위치를 오른쪽으로 1칸 민다. 곧, 텍스트에서 인덱스가 1인 문자와 패턴에서 인덱스가 0인 문자를 위아래로 나란히 놓는다. 위 그림처럼 첫 문자부터 검사에 실패한 후 다음 단계로 넘어간다.

 

3. 과정 5의 패턴을 검사하는 시작 위치를 오른쪽으로 1칸 민다. 곧, 텍스트에서 인덱스가 2인 문자와 패턴에서 인덱스가 0인 문자를 위아래로 나란히 놓는다. 패턴의 첫 문자부터 차례로 5, 6, 7의 과정처럼 검사하면 이번에는 모든 문자가 텍스트와 일치하여 검색에 성공한다.

 

과정 3에서는 텍스트쪽의 검사 위치가 2번 인덱스까지 나아갔지만 과정 4에서는 1번 인덱스로 되돌아오는 것을 볼 수 있다.

이처럼 이미 검사한 위치를 기억하지 못하기 때문에 브루트 포스법은 효율이 좋지 않다.

 

브루트 포스법 진행 순서

1. 각 문자열을 따라가는 커서를 선언
2. 문자열[커서]가 0이 아닐때 동안 반복
3. 만약 문자열[커서] == 문자열[커서]라면, 각 커서 + 1
4. 아니라면 pt는 pt - pp + 1부터, pp는 0부터 진행
5. 결과 반환은 만약 pp가 pat의 끝까지 비교했다면(전부 다 일치해서 pp의 길이와 같아진 상태) pt - pp를 반환, 아니면 -1 반환

 

브루트 포스법으로 문자열을 검색하는 코드

def bf_match(txt, pat):
    pt = 0  # txt를 따라가는 커서
    pp = 0  # pat를 따라가는 커서

    while pt != len(txt) and pp != len(pat):
        if txt[pt] == pat[pp]: 
            pt += 1
            pp += 1
        else:
            pt = pt - pp + 1
            pp = 0

    return pt - pp if pp == len(pat) else -1

if __name__ == "__main__":
    s1 = input("텍스트를 입력하세요: ")  # 텍스트용 문자열
    s2 = input("패턴을 입력하세요: ")   # 패턴용 문자열

    idx = bf_match(s1, s2)  # 문자열 s1 ~ s2를 브루트 포스법으로 검색

    if idx == -1:
        print("텍스트 안에 패턴이 존재하지 않습니다.")
    else:
        print(f"{(idx + 1)}번째 문자가 일치합니다.")

 

실행 결과

텍스트를 입력하세요: ABABCDEFGHA
패턴을 입력하세요: ABC
3번째 문자가 일치합니다.

Process finished with exit code 0

 

위 코드에서 bf_match( ) 함수는 텍스트 txt에서 패턴 pat를 검색한다. 그러면 검색에 성공한 txt 위치의 인덱스를 반환한다. 텍스트 txt 안에 패턴 pat가 여러 번 포함된 경우에는 가장 앞쪽에 위치한 인덱스를 반환한다. 검색에 실패한 경우에는 -1을 반환한다.

 

pt는 텍스트를 저장한 txt를 스캔하는 커서이다. 두 변수 모두 0으로 초기화하고 스캔을 하거나 패턴이 이동할 때마다 업데이트 된다.

 

이외에도 멤버십 연산자인 in과 not in으로 어떤 문자열이 다른 문자열 안에 포함되어 있는지 검색할 수 있고,

find, index 계열 함수로 검색한 문자열의 위치를 반환하는 방법도 존재한다.

 

멤버십 연산자로 구현

멤버십 연산자인 in과 not in을 사용하면 어떤 문자열이 다른 문자열 안에 포함되어 있는지 검색할 수 있다. 예를 들어 txt 안에 문자열 ptn이 포함되어 있는지 판단할 때에는 다음과 같이 수행한다.

ptn in txt		# ptn은 txt에 포함되어 있는가?
ptn not in txt		# ptn은 txt에 포함되어 있지 않는가?

 

이 방법을 이용하여 어떤 문자열이 다른 문자열 안에 포함되어 있는지 판단할 수는 있지만 그 위치(인덱스)는 알지 못한다.

검색한 문자열의 위치를 알고 싶다면 위 코드와 같이 배열을 사용해야 한다.

 

find, index 계열 함수로 구현

str 클래스형에 소속된 find( ), rfind( ), index( ), rindex( ) 함수는 문자열을 검색하여 검색한 문자열의 위치를 반환한다. 

아래 4가지 함수를 알아보자.

str.find(sub[, start [, end]])

• 문자열 str의 [start:end]에 sub가 포함되면 그 가운데 가장 작은 인덱스를 반환하고, 그렇지 않으면 -1을 반환한다.

find( ) 함수에서는 전달받은 인수 sub, start, end 중에서 end만 생략하거나 start와 end 둘 다 생략할 수 있다.

sub는 생략할 수 없다.(생략할 수 있는 인수 start와 end는 슬라이스 표기에 따라 지정한다.)

슬라이스 표기에 따라 start는 슬라이스의 시작 인덱스이며 기본값은 0이다. 또한 end는 슬라이스의 끝 인덱스이며 기본값은 슬라이스되는 시퀀스의 길이를 말한다.

[ ]는 그 안의 인수를 생략할 수 있다는 것을 나타내는 표기이다.

 

str.rfind(sub[, start [, end]])

• 문자열 str의 [start:end]에 sub가 포함되면 그 가운데 가장 큰 인덱스를 반환하고, 그렇지 않으면 -1을 반환한다. (생략할 수 있는 인수 start와 end는 슬라이스 표기에 따라 지정한다.)

 

str.index(sub[, start [, end]])

• 문자열 str의 [start:end]에 sub가 포함되면 그 가운데 가장 작은 인덱스를 반환하고, 그렇지 않으면 예외 처리로 ValueError를 내보낸다.

 

str.rindex(sub[, start [, end]])

• rfind( ) 함수와 같은 기능을 수행한다. 다만 sub가 발견되지 않으면 예외 처리로 ValueError를 내보낸다.

 

with 계열 함수로 구현

with 계열 함수는 어떤 문자열이 다른 문자열의 시작이나 끝에 포함되어 있는지를 판단한다.

str.startswith(prefix[, start [, end]])

• 문자열이 prefix로 시작하면 True, 그렇지 않으면 False를 반환한다. start가 지정되어 있으면 그 위치에서 판단을 시작하고, end가 지정되어 있으면 그 위치에서 비교를 중지한다.(start와 end는 생략 가능)

str.endswith(suffix[, start [, end]])

• 문자열이 suffix로 끝나면 True, 그렇지 않으면 False를 반환한다. start가 지정되어 있으면 그 위치에서 판단을 시작하고, end가 지정되어 있으면 그 위치에서 비교를 중지.(start와 end는 생략 가능)

startswith( ), endswith( ) 함수의 인수 start와 end는 생략할 수 있다.