[문자열 검색 알고리즘] KMP법

KMP법이란?

Knuth-Morris-Pratt법의 줄임말로 이 알고리즘을 고안한 크누스, 모리스, 프래트의 이름에서 따온 용어이다.

브루트 포스법은 일치하지 않는 문자를 만나면 다시 패턴의 첫 문자부터 검사를 수행하지만, KMP법은 검사 결과를 효율적으로 사용할 수 있다.

 

KMP법 알아보기

브루트 포스법은 일치하지 않는 문자를 만나면 이전 단계에서 검사했던 결과를 버리고 패턴의 첫 문자부터 다시 검색한다. 하지만 KMP법은 검사했던 결과를 버리지 않고 효율적으로 활용하는 알고리즘이다.

 

텍스트 'ZABCABXACCADEF'에서 패턴 'ABCABC'를 검색할 때 KMP법 알고리즘을 생각해보면 다음과 같다.

1. 먼저 위의 그림처럼 텍스트와 패턴의 첫 문자부터 차례로 검사를 수행한다. 텍스트의 첫 문자 'Z'는 패턴에 포함되지 않는 문자이므로 일치하지 않는다.

 

2. 이제 패턴을 오른쪽으로 1칸 민다. 그럼 위와 같이 비교하는데, 패턴의 앞쪽부터 차례로 검사를 수행해가면 패턴의 마지막 문자 'D'가 텍스트의 'X'와 일치하지 않는다. 

 

여기서 빨간색 문자로 나타낸 텍스트 안의 'AB'와 패턴안의 'AB'가 일치하는 것에 주목한다. 이 부분을 검사를 마친 위치라고 간주하면, 텍스트에서 'X' 이후 부분이 패턴의 'CABD'와 일치하는지 검사하면 된다.

그래서 아래 그림처럼 'AB'를 위아래로 나란히 놓고 패턴을 단 한 번에 오른쪽으로 3칸 밀어 3번째 문자 'C'부터 검사를 시작할 수 있다.

이처럼 KMP법은 텍스트와 패턴 안에서 겹치는 문자열을 찾아내 검사를 다시 시작할 위치를 구하여 패턴의 이동을 되도록이면 크게 하는 알고리즘이다. 그런데 몇 번째 문자부터 검사를 다시 시작할지 패턴을 이동할 때마다 계산한다면 좋은 효율을 기대할 수 없다.

그래서 KMP법은 '몇 번째 문자부터 다시 검색할지' 값을 표로 만들어서 문제를 해결한다.

 

아래 그림은 텍스트와 패턴이 불일치한 경우와 몇 번째 문자부터 검사를 다시 시작할지를 보여준다.

 

KMP법에서 사용하는 표 만들기

표를 작성할 때는 패턴에서 겹치는 문자열을 찾는다. 이 과정에서도 KMP법과 같은 방법을 적용한다. 패턴의 첫 문자가 일치하지 않으면 패턴을 오른쪽으로 1칸 밀어 첫 문자부터 검사해야 하므로 2번째 문자 이후 부분을 생각한다. 또 패턴과 텍스트를 서로 겹치도록 맞추는 것이 아니라 패턴끼리(즉, 패턴과 패턴을) 서로 겹치도록 맞추고 검사를 시작할 곳을 계산한다. 표를 작성하는 순서는 다음과 같다.

 

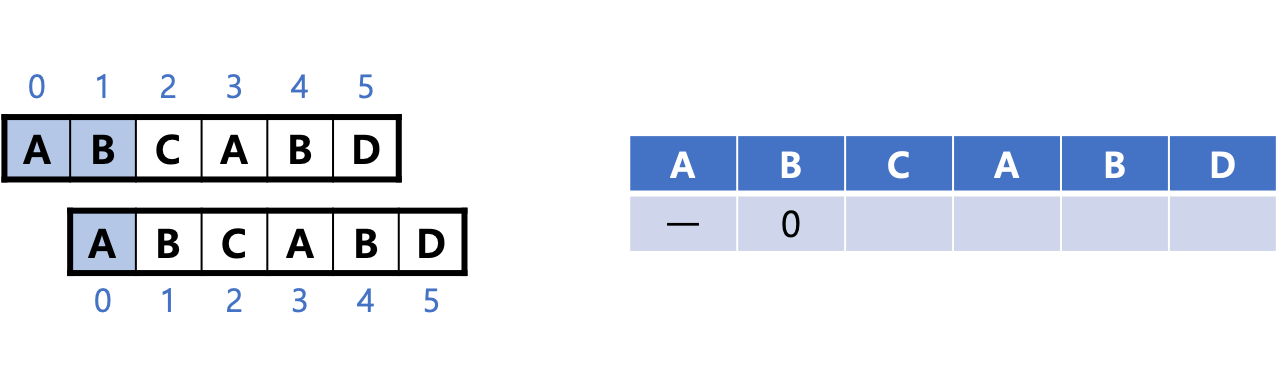
1. 패턴 'ABCABD' 2개를 위 아래로 나란히 놓고 아래쪽 패턴을 오른쪽으로 1칸 밀어 서로 겹친다. 다음 그림에서 파란색 부분이 일치하지 않으므로 아래쪽 패턴을 이동하면첫 문자부터 검사를 다시 시작해야 한다는 것을 알 수 있다. 그러므로 텍스트에서 2번째 문자 'B'는 다시 시작하는 값을 0으로 한다.

패턴의 첫 문자 인덱스는 0이다. 그 위치부터 검사를 다시 시작하기 때문이다.

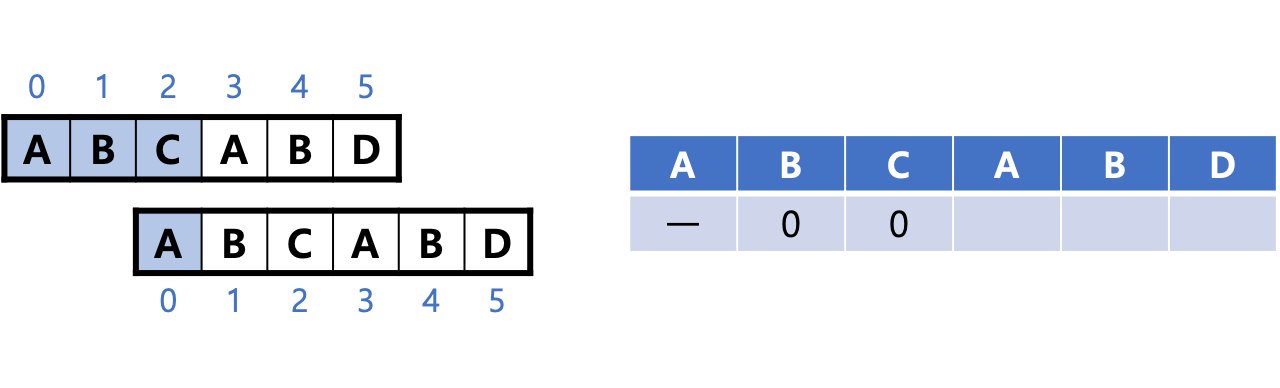
2. 패턴을 오른쪽으로 1칸 민다. 마찬가지로 문자가 일치하지 않으므로 텍스트에서 3번째 문자 'C'는 다시 시작하는 값을 0으로 한다.

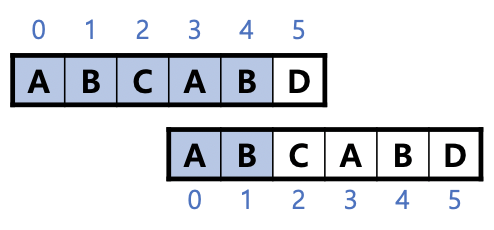
3. 패턴을 오른쪽으로 1칸 밀면 'AB'가 일치하는데, 여기서 다음과 같은 사실을 알 수 있다.

• 패턴의 4번째 문자 'A'까지 일치하는 경우: 패턴 이동 후 'A'를 건너뛰고(skip) 2번째 문자부터 검사할 수 있다.
• 패턴의 5번째 문자 'B'까지 일치하는 경우: 패턴 이동 후 'AB'를 건너뛰고(skip) 3번째 문자부터 검사할 수 있다.

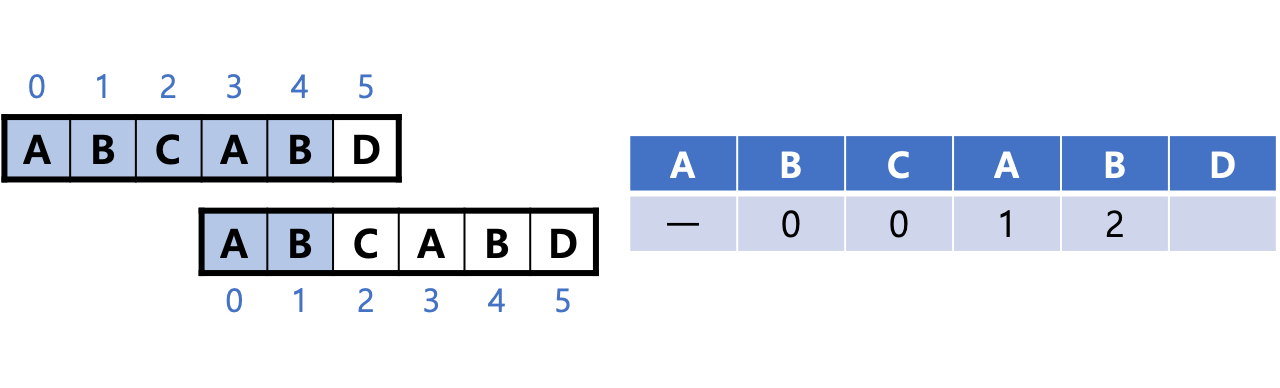
그러므로 'A'와 'B'는 다시 시작하는 값을 표에서 각각 1과 2로 작성한다.

 

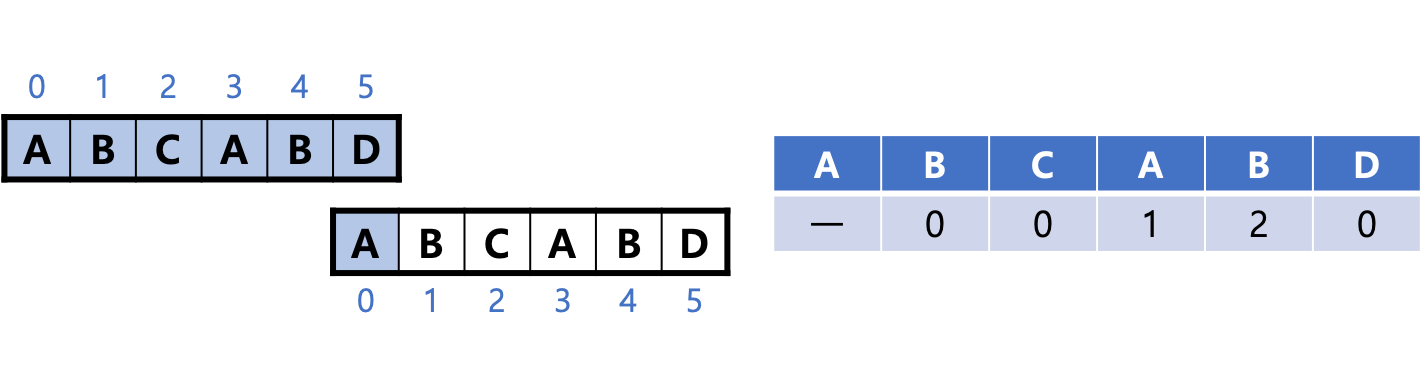
4. 이어서 패턴을 오른쪽으로 2칸 밀면 문자가 일치하지 않는다. 그래서 패턴의 끝 문자 'D'는 다시 시작하는 값을 0으로 작성한다.

이로써 표가 완성되었고, 이렇게 작성한 표는 건너뛰기 표(skip table)라고 부른다.

 

KMP법으로 문자열 검색하기

# KMP법으로 문자열 검색하기

def kmp_match(txt: str, pat: str) -> int:
    """KMP법으로 문자열 검색"""
    pt = 1 # txt를 따라가는 커서
    pp = 0 # pat를 따라가는 커서
    skip = [0] * (len(pat) + 1) # 건너뛰기 표

    # 건너뛰기 표 만들기
    skip[pt] = 0
    while pt != len(pat):
        if pat[pt] == pat[pp]:
            pt += 1
            pp += 1
            skip[pt] = pp
        elif pp == 0:
            pt += 1
            skip[pt] = pp
        else:
            pp = skip[pp]

    # 문자열 검색하기
    pt = pp = 0
    while pt != len(txt) and pp != len(pat):
        if txt[pt] == pat[pp]:
            pt += 1
            pp += 1
        elif pp == 0:
            pt += 1
        else:
            pp = skip[pp]

    return pt - pp if pp == len(pat) else -1

if __name__ == "__main__":
    s1 = input("텍스트를 입력하세요.: ") # 텍스트용 문자열
    s2 = input("패턴을 입력하세요.: ")  # 패턴용 문자열

    idx = kmp_match(s1, s2) # 문자열 s1 ~ s2까지를 KMP법으로 검색

    if idx == -1:
        print("텍스트 안에 패턴이 존재하지 않습니다.")
    else:
        print(f"텍스트안에 문자열이 {idx + 1}번째 위치에 있습니다.")

 

실행 결과

텍스트를 입력하세요.: ABABCDEFGHA
패턴을 입력하세요.: ABC
텍스트안에 문자열이 3번째 위치에 있습니다.

Process finished with exit code 0

 

KMP법으로 kmp_match( ) 함수가 전달받는 인수와 반환값은 브루트 포스법으로 bf_match( ) 함수가 전달받은 것과 같다.

 

위 코드의 건너뛰기 표를 만드는 부분은 다시 시작하는 값을 건너뛰기 표로 만들고, 실질적으로 문자열을 검색하는 부분은 문자열 검색을 수행한다.

KMP법에서 텍스트를 스캔하는 커서 pt는 앞으로 나갈 뿐 뒤로 되돌아오지 않는다. 이것은 브루트 포스법에는 없는 특징이다.

그러나 KMP 알고리즘은 복잡할 뿐, 보이어-무어법 보다 성능 면에서 같거나 오히려 낮은 수준이기때문에 실제 프로그램에서 별로 사용하지 않는다.